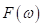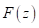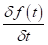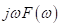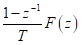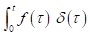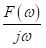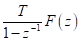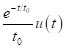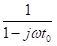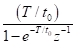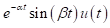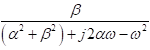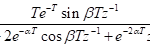Full waveform inversion (FWI) is a non-linear optimization procedure which can derive high resolution models by minimizing the misfit between the observed and simulated waveforms. This definition indicates the essence of FWI is utilizing the information of observed full waveform during the inversion. Generalized speaking, any optimization procedure using the full waveform information can be called as FWI. Before giving the outlooks of GPR FWI, let’s first figure out what kind of problems is hindering the improvement of this method? Same as other geophysical methods, the final goal of FWI progress is to improve its capability for practical applications or in other words, provides the geophysical evidence for solving the problems of geology, hydrology or engineering etc. Hence, the obstructions of FWI mainly come from its improvable theory and the application limits (I will explain these more detailed later). Other interferences like the limitation of equipment and computational power etc. are also important for FWI but not the key issues for this essay.
1. Theory part
There are two key elements of FWI—forward and inversion, which have different emphasis of research direction. Because of the development of computer, modern physics is more and more depending on the simulation technique and a new discipline called computational physics (CP) has been known gradually. Geophysical forward in FWI is only a small part of the CP, which is to generate the simulated data by solving the wave equations (Maxwell’s equations for GPR). The development of forward in FWI mainly focused on utilizing the advanced CP techniques for geophysical purposes (see Fig. 1). Due to the backward state of geophysical forward compared to modern CP technique, there still have great potential to improve it. However, the ceiling of this improvement also exists which is the inversion method of FWI. Inversion in FWI is to calculate the misfit between simulated and observed data and give the update direction of models (see Fig. 1).
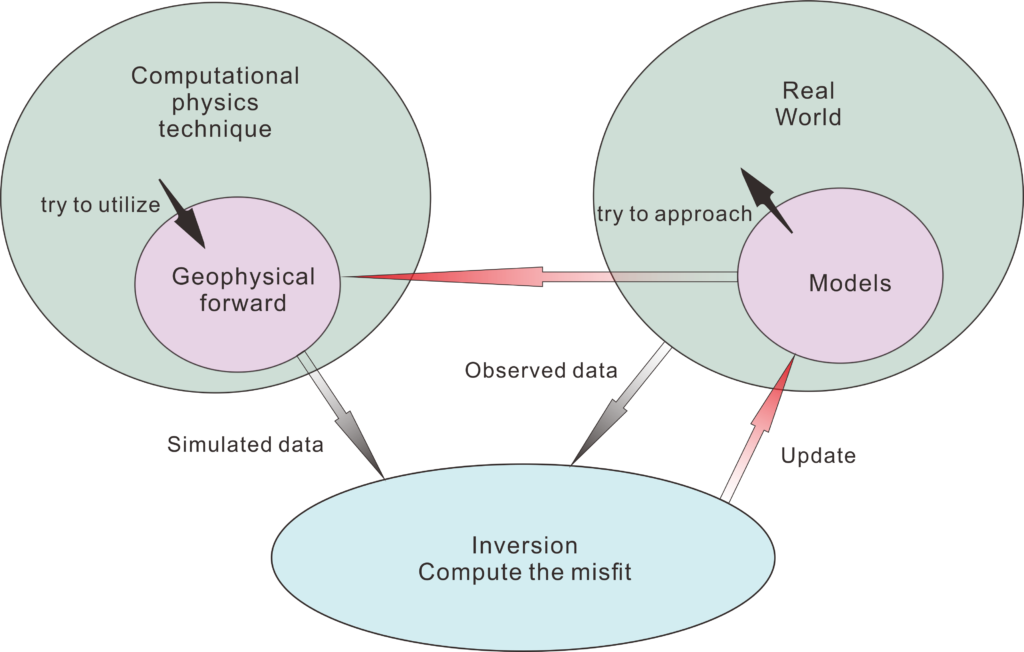
We must admit there is a huge gap between the development of forward and inversion. Theoretically FWI should consider all the physical phenomenon of wave propagation. However, it is impossible in practice due to the non-linearity and ill-posedness of FWI algorithm. This means many advanced forward techniques are not suitable for the current theory of inversion (an example will be given later). In fact, the geophysicists mainly focus on inversion methodology research and try to improve its theory for raising the ceiling of utilizing more advanced forward techniques, for example, the proposed method of FWI itself. Therefore, we must note there is a lot of ways to improve the FWI and the improvement of the entire FWI method is a step-by-step process.
2. Forward problem
FWI is a non-linear local optimization procedure which means the inversion needs to call forward operation several times during a single iteration and totally hundreds of times forward operation are needed for the entire procedure. Moreover, due to the limited computational resources and the development of acquisition systems which make the long-offset, large-scale 3D even 4D data more feasible, the most important characteristic of forward in FWI is the high efficiency. Meanwhile, the forward modeling also need to be quite accurate because FWI can provide higher resolution (half a wavelength) imaging compared to conventional inversion methods. Therefore, a reasonable conjecture about the future development direction of forward in FWI is to propose high efficiency and accuracy algorithms which are suitable for the modern geophysical acquisition techniques, thus can help to obtain high resolution results close to the real world (Fig. 1).
Despite various techniques have been developed and applied for the forward problem of GPR, such as the finite-volume method (FVM) (Shankar et al., 1989), finite-element method (FEM) (Jin, 2014), transmission-line matrix method (Christopoulos, 2006), pseudospectral method (Qing Huo, 1999) and the method of moments (Harrington, 1993). The modern GPR FWI is mostly based on the finite-difference method both in time (FDTD) and frequency domain (FDFD) (Meles et al., 2010, Lavoue et al., 2014). The finite-difference method is a direct numerical approximation of the wave equation which has several advantages compared with other methods: it has clear physical meaning and easy to implement; it is efficient and relative stable; the computational time for a given grid size is independent of the model complexity; it is suitable to treat impulsive behavior of the electromagnetic field and can provide either ultra-wide-band temporal waveforms or the sinusoidal steady-state response at any frequency within the excitation spectrum (Benedetto and Pajewski, 2015); and it is amenable to a very high level of fine-gain parallelism. (The discussion of the differences between time domain and frequency domain approach for instance FDTD and FDFD will be given later)
High-order discretization scheme
As is well known, the conventional FDTD method based on Yee’s mesh has the second-order accuracy central difference approximation both in spatial and temporal derivatives, and it can provide excellent result for small scale problem. However, when the scale getting larger both the length of time integration and the number of grid points have to increase which means the influences of numerical dissipation and dispersion cannot be ignored anymore. Moreover, the lossy and dispersive effects caused by materials such as metal or soil, and the discontinuous material interface also need to be considered for the practical GPR measurement simulation. It is therefore desirable to utilize high-order schemes to solve these kinds of problems. The high-order schemes can be applied both in spatial and temporal derivatives for providing higher accuracy (lower phase and amplitude errors) and faster convergence rate, respectively. Note that, here I will not discuss too much detail about the high-order algorithms because it has been the subject of a very comprehensive and elaborate study including absorbing boundary derivation, the conventional form and nonstandard form (not using Yee’s mesh), or even hybrid scheme (using fine mesh) etc. There are many instructive books described the high-order FDTD exhaustively such as Kantartzis and Tsiboukis (2005).
Despite many high-order algorithms have been proposed for GPR simulation such as the most broadly implemented FDTD (2, 4) and FDTD (4, 4) schemes (Hadi and Piket-May, 1997, Bergmann et al., 1998, Teixeira et al., 1998). To the best of my knowledge, there are not any works on using the high-order forward for GPR data FWI. However, many high-order forward based FWI have been reported in seismic data inversion (Plessix, 2009, Brossier, 2011). Considering the similarity between seismic and EM waves propagation, it is quite promising to propose a FWI method based on high-order forward schemes for GPR data, for instance the measurement on dispersive, inhomogeneous, and conductive soils.
Unstructured mesh
An obvious disadvantage of finite-difference method is the usage of regular grid which leads to a staircase-like discretization (see Fig. 2a as a 2D example).

Such discretization is not suitable for the boundary conditions of complex geometries and interfaces of three-phase media (partially saturated with water and air) because the inaccurate approximation can bring errors into the final simulation results; for instance the parasite diffractions from the corners of the rectangular grid. One solution is using the fine discretization; however, due to the constant interval of regular grid the fine discretization generally leads to local oversampling of the calculation area, and therefore a waste of computational resources and time.
To overcome the disadvantages of regular grid the unstructured grid based methods can be used, such as FEM and FVM. Unstructured grid especially triangular/tetrahedral meshes can handle complex geometries and allow strong physical contrasts in the medium (see Fig. 2b), because the element boundaries coincide with the boundary between different media. That means no interpolation and averaging of physical properties is necessary and all the properties can be defined on each element and not on individual nodal points. Moreover, the unstructured grid allows fine discretization close to the boundary of different media without the need of a dense mesh for the entire calculation area (see Fig. 2c). This leads to accurate simulation results with a much smaller number of total grid points compared to the regular grid and therefore also to higher efficiency especially for 3D problem.
Despite from a programming point of view the unstructured grid based methods (FVM and FEM) are more complex compared to FDM; the high accuracy results provided by those methods are still quite impressive. Moreover, several techniques like hp-adaptive, Discontinuous Galerkin (DG) method (Brossier, 2011) and hybrid FEM-FDM (using the FEM in space and the explicit FDM in time) (Frehner et al., 2008) can make the simulation more efficient which means the unstructured grid based methods are also suitable as the forward method of GPR data FWI.
3D simulation
2D problem is a simplification of the realistic 3D world, for converting the simulation of GPR signal propagation from 3D to 2D many assumptions have been made in different aspects for instance using the 2D acquiring or processing method, assuming a homogeneous isotropic medium and using line source or far field approximation etc. However, those assumptions may lead the inversion to the wrong results due to the non-unicity when we use 3D measured data for a 2D FWI (see Fig. 1). Therefore more information from the real measurement are needed to be involved for the inversion such as the polarimetric radar information, the vector-valued waves scattering and antenna radiation patterns etc. Which means a full waveform modeling in 3D is necessary for future FWI.
Two major issues are obstructing the development of 3D simulation of GPR/seismic measurement:
a) accuracy
Theoretically it’s impossible to represent the realistic 3D world perfectly by only using the mathematical methods. What we do is trying our best to make the mathematical tools as complicated as possible to provide an approximate result. For instance including the heterogeneous anisotropy medium or polarization tensors for the scattering of perfectly conducting objects or developing solvers for the frequency dependence materials etc. Indeed for different scales (frequency bands) the mathematical tools been used also should be different and have their own emphasis. For instance at very high frequency (optical band) the simulation needs to include the non-linearity and the quantum effect. One of the hot spots for 3D simulation today is the study of multi-physical field coupling which can promote the development for multidisciplinary such as the material science, energy science & engineering etc. In geophysical application there also have a branch called co-seismic electromagnetic fields which describing the electromagnetic anomalies associated with seismic waves.
b) efficiency
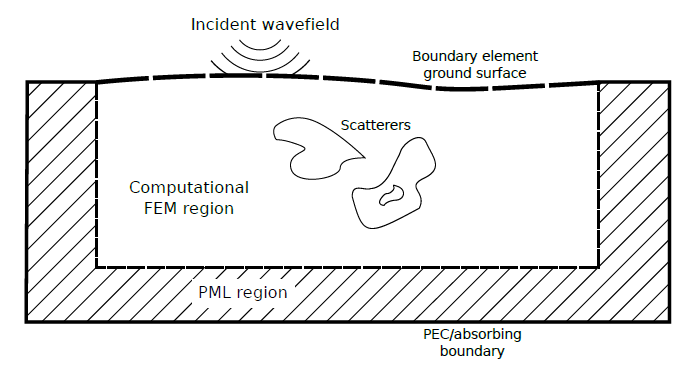
High efficiency is an eternal goal for numerical simulation. During last decades lots of fast algorithms have been proposed and utilized, for instance the surface integral equation (SIE) solved by the method of moments (MoM) and its fast algorithm the multilevel fast multipole algorithm (MLFMA) (Song et al., 1997). Despite the SIE is not suitable for geophysical inversion because this method only calculates the EM field on the surface of the simulation target, there still have a solution by using a combined strategy (see Fig. 3) (Watson, 2016). Such strategy needs to calculate the equivalent sources then the whole area can be separated to several number of parts (every part needs an equivalent source) and parallel calculated on the cluster. The advantages of MoM then can be used for GPR FWI such as MLFMA and no PML is needed during forward modeling. Moreover, the FWI for large scale problem become possible. However, this strategy needs to calculate a large dense matrix which is not efficient. Moreover, the singularity of such dense matrix also can cause failure of solving it.
Solving large matrix will bring us to another subdiscipline called equation solvers; and lots number of direct solver, iterative solver or combined strategy have been proposed. Also, many techniques have been developed such as precondition, singular-value decomposition (SVD), hierarchical LU factorization and the most recent the butterfly scheme (Guo et al., 2017) etc. (will not discuss the details of the solvers here)
Combined with Laplace Transform, Z-transform and s-transform etc.
Since the numerical simulation methods have been proposed people are trying to improve them for simulations of more complex situations such as the frequency-dependent medium (effects of electromagnetic radiation on human brain) or joint numerical simulation of multi-physical fields (behaviors of electromagnetic waves directly excited by earthquakes) etc. For improving the methodology of simulation technique itself, one direction is utilizing the methods that been used by system and signal processing engineers when dealing with discrete time signals, like Laplace transform, Z-transform, s-transform and wavelet transform etc. The main idea is making the simulation more intuitive and effective for particular problems, also a more concise formulation of the problem can be given (good for coding) (Sullivan, 1992). Here is a comparison between the time, frequency and Z-domains.
Time Domain | Frequency Domain | Z Domain |
|---|---|---|
| 1 | 1 |
|
Supplement
We need to notice that there are similarities and differences between GPR and seismic FWI.
- GPR has large order of magnitude attenuation coefficient compared to seismic (sigma vs. Q).
- Seismic FWI has more cross-talk (more parameters to invert) compared to GPR FWI.
The similarities (problems make the inversion fail) most come from the FWI method itself, more details will be discussed in next blog.
References
Benedetto, A. & Pajewski, L., 2015. Civil Engineering Applications of Ground Penetrating Radar, edn, Vol., pp. Pages, Springer International Publishing.
Bergmann, T., Robertsson, J.O.A. & Holliger, K., 1998. Finite‐difference modeling of electromagnetic wave propagation in dispersive and attenuating media, Geophysics, 63, 856-867.
Brossier, R., 2011. Two-dimensional frequency-domain visco-elastic full waveform inversion: Parallel algorithms, optimization and performance, Computers & Geosciences, 37, 444-455.
Christopoulos, C., 2006. The Transmission-Line Modeling (TLM) Method in Electromagnetics, edn, Vol., pp. Pages, Morgan & Claypool.
Frehner, M., Schmalholz, S.M., Saenger, E.H. & Steeb, H., 2008. Comparison of finite difference and finite element methods for simulating two-dimensional scattering of elastic waves, Physics of the Earth and Planetary Interiors, 171, 112-121.
Guo, H., Liu, Y., Hu, J. & Michielssen, E., 2017. A Butterfly-Based Direct Integral-Equation Solver Using Hierarchical LU Factorization for Analyzing Scattering From Electrically Large Conducting Objects, IEEE Transactions on Antennas and Propagation, 65, 4742-4750.
Hadi, M.F. & Piket-May, M., 1997. A modified FDTD (2, 4) scheme for modeling electrically large structures with high-phase accuracy, IEEE Transactions on Antennas and Propagation, 45, 254-264.
Harrington, R.F., 1993. Field computation by moment methods, edn, Vol., pp. Pages, Wiley-IEEE Press.
Jin, J.-M., 2014. The Finite Element Method in Electromagnetics, 3rd edn, Vol., pp. Pages, John Wiley & Sons, Hoboken.
Kantartzis, N.V. & Tsiboukis, T.D., 2005. Higher order FDTD schemes for waveguide and antenna structures. in Synthesis Lectures on Computational Electromagnetics, pp. 1-226.
Lavoue, F., Brossier, R., Metivier, L., Garambois, S. & Virieux, J., 2014. Two-dimensional permittivity and conductivity imaging by full waveform inversion of multioffset GPR data: a frequency-domain quasi-Newton approach, Geophysical Journal International, 197, 248-268.
Meles, G.A., Van der Kruk, J., Greenhalgh, S.A., Ernst, J.R., Maurer, H. & Green, A.G., 2010. A New Vector Waveform Inversion Algorithm for Simultaneous Updating of Conductivity and Permittivity Parameters From Combination Crosshole/Borehole-to-Surface GPR Data, IEEE Transactions on Geoscience and Remote Sensing, 48, 3391-3407.
Plessix, R.É., 2009. Three-dimensional frequency-domain full-waveform inversion with an iterative solver, Geophysics, 74, WCC149-WCC157.
Qing Huo, L., 1999. Large-scale simulations of electromagnetic and acoustic measurements using the pseudospectral time-domain (PSTD) algorithm, IEEE Transactions on Geoscience and Remote Sensing, 37, 917-926.
Shankar, V., Hall, W.F. & Mohammadian, A.H., 1989. A time-domain differential solver for electromagnetic scattering problems, Proceedings of the IEEE, 77, 709-721.
Song, J., Cai-Cheng, L. & Weng Cho, C., 1997. Multilevel fast multipole algorithm for electromagnetic scattering by large complex objects, IEEE Transactions on Antennas and Propagation, 45, 1488-1493.
Sullivan, D.M., 1992. Frequency-dependent FDTD methods using Z transforms, IEEE Transactions on Antennas and Propagation, 40, 1223-1230.
Teixeira, F.L., Weng Cho, C., Straka, M., Oristaglio, M.L. & Wang, T., 1998. Finite-difference time-domain simulation of ground penetrating radar on dispersive, inhomogeneous, and conductive soils, IEEE Transactions on Geoscience and Remote Sensing, 36, 1928-1937.
Watson, F.M., 2016. Better Imaging for Landmine Detection: An exploration of 3D full-wave inversion for ground-penetrating radar, Doctor, The University of Manchester.