Definition of benchmark
- something that serves as a standard by which others may be measured or judged
- a point of reference from which measurements may be made
- a standardized problem or test (whose quality or quantity is known) that serves as a basis for evaluation or comparison
For a geophysical application purpose the benchmark data/model is mainly been designed for testing the forward/inversion algorithm. It is very like the opposite of benchmark definition in computer science “the act of running a computer program, a set of programs, or other operations, in order to assess the relative performance of an object, normally by running a number of standard tests and trials against it.” (Wikipedia) The difference is in computer science benchmark is usually associated with assessing performance characteristics of computer hardware, while in geophysics benchmark is used for evaluating the “software”.
The main feature of a benchmark is the quality of the data/model should be well known. People use it as a standard, then any evaluation or comparison based on it can be accepted very quickly. A good benchmark must be withstood the test of time, because pursuing a new benchmark includes a lot of repeating work and in a sense squanders our resources (time, energy etc.). However, in geophysics creating and pursuing a new benchmark is not a very difficult goal, because people have a consensus about the standard, any outrageous results will not be accepted. Besides for a comparison the control algorithm must been test by the well-known benchmark which provided a link of the new created benchmark to old qualified benchmark. The only thing you need to consider is does it really necessary?
A good benchmark should be focused on its purpose, witch means for different evaluation or comparison we may use different benchmark. This also explained why there are so many benchmark data sets/models for geophysical methods. Various applications need numerous benchmark, yet we still can create a very complex benchmark contain many purposes to show how powerful of our algorithm. But just remember “One solution can not solve all the problems”.
-
Fully synthetic benchmark
This kind of models mostly use very simple structures, shapes and parameters, because simple things naturally satisfy the well-known condition of benchmark, hence much easier and faster been accepted by people. The expected results of the new algorithm to this kind of models is as close as possible to the results of control algorithm or analytic solution, because the fully synthetic benchmark model is used to test the algorithm or code “working well”. This is step one of giving a rigorous comparison when writing a paper to propose a new geophysical algorithm. Below are some examples of the fully synthetic benchmark model (1D, 2D & 3D):

However, people also can increase the complexity of benchmark models by sacrificing the acceptability in certain aspects. For example, much more complex shapes or parameters to show the capability of new algorithm. This kind of benchmark models are still far away from the reality situation but in some extent they can be seen as an extreme case of real data. The prerequisite by doing so is the gain should be much larger than the sacrifice, because one may take the risk of getting questions about the models which means more extra works for the explanation and slower acceptance of the new algorithm. This also can be considered as the step two for writing a paper to propose a new geophysical algorithm but it is not a necessary choice. Here I give tow examples, the first one comes from Meles et al., 2011.
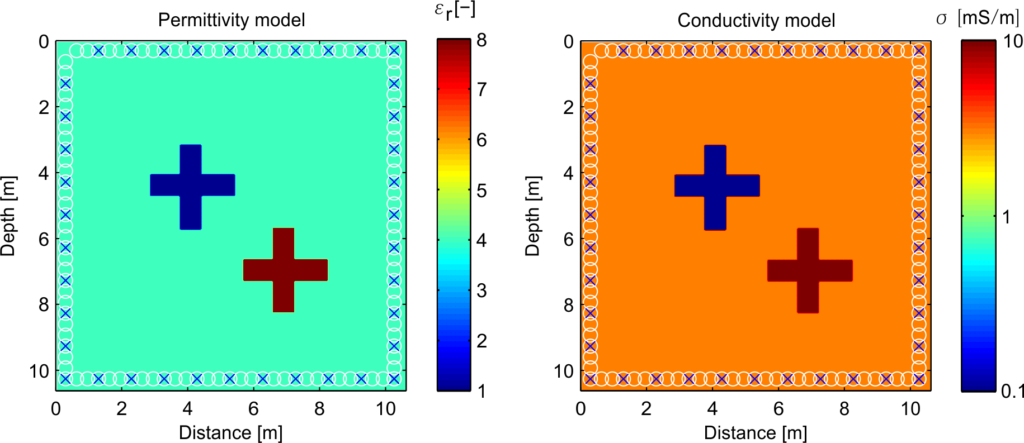
This model contain two complex shape abnormal targets in homogeneous background and more important is the high contrast parameters of which can make conventional FWI failed due to the non-linear problem. Moreover, because of the property of GPR data, multi-parameter inversion is unavoidable; therefore, cross-talk between parameters also make this model quite challenging. Good news is because this model has been used to investigate the non-linear problem of GPR FWI quite early, more and more people accepted it and used it in their own papers.
The second example comes from Irving et al., 2009. The purpose of this model is to simulate the underground truth by using stochastic models. The properties of real data including heterogeneous and anisotropy can be presented by this kind of benchmark models. More convenient thing is by repeating the simulation of different degree of randomness an assessment of the ensemble uncertainty can be determined. Note that, the two figures shown water content distribution and wave velocity field respectively according to the relationship between dielectric permittivity and porosity: \kappa = \frac{{{c^2}}}{{{v^2}}}, and \theta = \frac{{\sqrt \kappa - \sqrt {{\kappa _s}}}}{{\sqrt {{\kappa _w}} - \sqrt {{\kappa _s}}}}. Which leads to another characteristic of benchmark, the model parameter should be easy to convert to another parameter (usually from physical parameters to petrophysics parameters). However, we should notice that this conversion aims to link two different methodologies (measurement) and we need to avoid this situation as much as possible, because it always contained assumption and statistical errors in there.

-
Realistic synthetic benchmark
After step one and step two, we finally get to step three: evaluate our new algorithm can still “working well” for real measurement data. There are two options for step three: use real data or realistic synthetic benchmark. For writing a paper to propose a new geophysical algorithm, real data never be the first choice. Because we never know the underground truth from the observed data which means we can not have the direct comparison, however the indirect comparison needs lots of evidence and verifying from the other measurements. With all of these, we can write a paper of case study already besides it’s quite hard to focus on the algorithm itself. That’s why the realistic synthetic benchmark is very important for geophysicist.
The realistic synthetic benchmark mainly comes from the industry and been supported by lots of evidence which means it’s quite close to the underground truth. A good realistic synthetic benchmark should be qualified by a set of strict standards (with standard format) and supervised by a proprietary database as an open source data. Therefore, here I have to mention the SEG advanced modeling (SEAM) corporation. SEAM is a partnership between industry and SEG designed to advance geophysical science and technology through the construction of subsurface models and generation of synthetic data sets. The SEAM projects provide the geophysical exploration community with geophysical model data at a level of complexity and size that cannot be practicably computed by any single company or small number of companies. Unfortunately most SEAM data is seismic data, and the open near surface data is still in development.
In fact, lots of well maintained exploration geophysical datasets can quite easy to be downloaded and used from organizations like SEG and EAGE. For instance the 2004 BP Velocity-analysis Benchmark dataset and the SEG/EAGE 3D Salt Model Phase-C 1996.

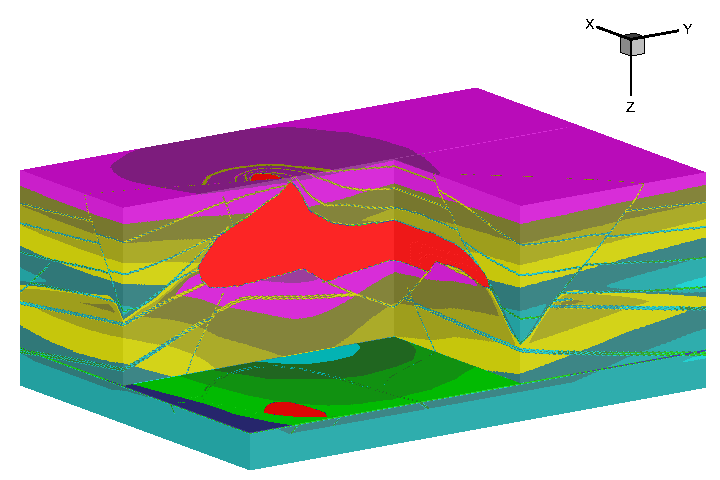
And of course the quite famous Marmousi model, which was generated at the Institute Francais du Petrole (IFP), and was used for the workshop on practical aspects of seismic data inversion at the 1990 EAEG meeting. Marmousi model has become a popular testbed for inversion algorithms such as migration and FWI. “One of the biggest contributions of the Marmousi model is that it demonstrated the limitations of first-arrival traveltimes in imaging complex media. Specifically, Geoltrain and Brac (1993) showed that to properly image the Marmousi model we need multi-arrival traveltimes.” (Quoted from Tariq Alkhalifah)

However, the successes of seismic benchmark can not be copied to other geophysical methods such as GPR or EMI, because it needs lots of support from the industry. So we back to seek the second choice which is we scaling the seismic benchmark by a factor. This is the smallest influence we can achieve to convert the original benchmark for other geophysical method applications. For instance scaling the SEG/EAGE overthrust model to a GPR benchmark.
Parameter | Seismic scale | On-ground GPR scale |
|---|---|---|
Lx , Lz | [20.0, 4.65] (km) | [12.07, 2.82] (m) |
Vp/permittivity | [2.36, 6] (kms−1) | [2.36, 6]•ε0 (F/m) |
Attenuation/conductivity | / | [0.1, 10] (mS/m) |
Frequency range | [1.7, 7.0] (Hz) | [100, 400] (MHz) |
/lamda | [0.6, 2.46] (km) | [0.75, 3] (m) |

After all, there is a long and successful history of employing standard seismic processing and algorithm to GPR data inversion.
-
Fully functional synthetic benchmark
Note that, the realistic synthetic benchmark I mentioned above is still far away from the underground truth. From the inversion point of view, those benchmark models for testing algorithms only take a part of the full picture. The real function of a benchmark for geoscience is giving a numerical version of the underground truth for the modeling tools, and evaluating the time-lapse forward results with the observed data sets for monitoring the changes, very like a large scale digital rocks project. Which means a fully functional synthetic benchmark must be quite complex and integrate different disciplines such as geology, petrophysics, hydrology or even biology. Inversion of such kind of model is a very challenging target, some combined inversion strategy can be utilized for this purpose. For instance the Stanford VI-E reservoir, a large-scale data set including time-lapse (4D) elastic attributes and electrical resistivity is generated with the purpose of testing algorithms for reservoir modeling, reservoir characterization, production forecasting, and especially joint time-lapse monitoring using seismic as well as electromagnetic data.

Summary
Now we back to the initial question: what characteristics should be qualified for a good synthetic benchmark model? The answer is actually depends on the studied physical phenomena. Here I only list a qualified benchmark synthetic model for evaluating a forward/inversion algorithm, which should have the following characteristics:
- agree with people’s consensus
- can be accepted fast
- focus on its purpose
- good balance of challenging (withstand the test of time)
- (parameters) are easy to convert
- use standard format and be well maintained
- to some extent close to the underground truth