In applied mathematics, discontinuous Galerkin methods (DG methods) form a class of numerical methods for solving differential equations. They combine features of the finite element and the finite volume framework and have been successfully applied to hyperbolic, elliptic, parabolic and mixed form problems arising from a wide range of applications. DG methods have in particular received considerable interest for problems with a dominant first-order part, e.g. in electrodynamics, fluid mechanics and plasma physics.
MFEM
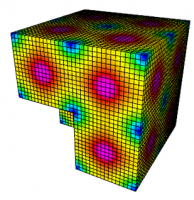
MFEM is a free, lightweight, scalable C++ library for finite element methods.
The goal of MFEM is to enable research and development of scalable finite element discretization and solver algorithms through general finite element abstractions, accurate and flexible visualization, and tight integration with the hypre library.
Conceptually, MFEM can be viewed as a finite element toolbox that provides the building blocks for developing finite element algorithms in a manner similar to that of MATLAB for linear algebra methods.
Link (2016/7/26)
Link (2016/7/26)
Link (2016/7/26)
NekCEM
In the software package NekCEM (Nekton for Computational ElectroMagnetics) the spectral element discontinuous Galerkin (SEDG) method is employed on a conformal spectral-element mesh. NekCEM features geometric flexibility, spectrally accurate numerical convergence, and an efficient parallel implementation.
This package consists of the components of meshing, Maxwell time domain solver, electrostatic poisson solver, and visualization tools. It supports the computational domain boundary with perfectly matched layer, perfect conductor, and periodic material.
Link (2016/7/22)
Link (2016/7/22)
Link (2016/7/22)
NekCEM is based on Nek5000 which is an open source, highly scalable and portable spectral element code designed to simulate unsteady Stokes, unsteady incompressible Navier-Stokes, low Mach-number flows, heat transfer and species transport, incompressible magnetohydrodynamics (MHD).
Features
- scales to over a million processes
- high-order spatial discretization using spectral elements
- high-order semi-implicit timestepping
- incompressible + low Mach number (variable density) flows
- efficient preconditioners (multigrid + scalable coarse grid solves)
- highly optimized computational kernels (e.g. matrix-matrix multiply)
- low memory footprint and scalable memory design
- high performance parallel I/O
- ALE / moving meshes and free surface flow
- accurate Lagrangian particle tracking
- conjugate fluid-solid heat transfer
- scalable communication kernels
- build-in profiling analysis
- interface to VisIt for parallel data analysis and visualization
- interace to MOAB for advanced meshing capabilities
Link (2016/7/27)
hpGEM
hpGEM is a C++ software package for discontinuous Galerkin method. This framework is intended to those who want to easily develop and apply discontinuous Galerkin methods for various physical problems, especially partial differential equations, arising from fluid mechancis and electro-magnetism. Using HPGEM, one can numerically solve the simplest class room examples such as linear advection and Burgers equations to the most complicated practical examples such as shallow water, Euler, Navier-Stokes and Maxwell equations.
Link (2016/7/22)
Link (2016/7/22)
MAXDGTD
MAXDGTD is a discontinuous Galerkin code for solving Maxwell’s equations in the time-domain.
The discontinuous Galerkin code uses a combination of high-order spatial and various temporal discretizations methods.

Link (2016/7/22)
Hedge
hedge is an unstructured, high-order, parallel Discontinuous Galerkin (DG) code. It takes a hybrid approach. While a small core is written in C++ for speed, all user-visible functionality is driven from Python.
Link (2016/7/22)
Link (2016/7/22)
Link (2016/7/22)
nodal-dg
nudg: Nodal Unstructured Discontinuous Galerkin methods. This is an extensively developed software package, providing both Matlab and C++ software, for method components and a large number of application examples solved using discontinuous Galerkin methods on unstructured grids. The Matlab software is extensively documented in the text Nodal Discontinuous Galerkin Methods and the C++ code (named nudg++) provides a C++ mirror of these codes to enable enhanced efficiency and flexibility beyond Matlab.

Link (2016/7/22)
Link (2016/7/22)
MIDG2
MIDG2 is a time-domain Maxwell’s solver based on discontinuous Galerkin discretization in space and low-storage Runge-Kutta discretization in time accelerated by the OCCA2 extensible many-core programming interface. Capabilities include: Maxwell’s equations solved in 2D and 3D on unstructured grids, hybrid MPI+OCCA2 parallelism.

Link (2016/7/25)
MIDG
MIDG is a very lightweight C based code treatment for the time-domain Maxwell’s discontinuous Galerkin solvers in 2D and 3D. It can run on GPU+MPI or CPU+MPI written by Tim Warburton.
MIDG does the following:
1.distributed loading of a mesh file
2.calls ParMETIS to partition the mesh, on the fly, with load balancing and communication quasi-minimization
3.uses a parallel sort to set up inter-element connectivity
4.time steps using a low storage Runge-Kutta scheme

Link (2016/7/26)